- Запишите блок-схему с 1 входной переменной, вычисляющей ее факториал.
- Запишите блок-схему с 2 входными переменными, вычисляющую количество простых чисел между ними.
- На рисунке изображена блок-схема, приведены несколько спецификаций. Домены всех переменных - множество всех целых чисел. Ответьте на вопрос про каждую из спецификаций, является ли эта блок-схема частично корректной относительно неё?
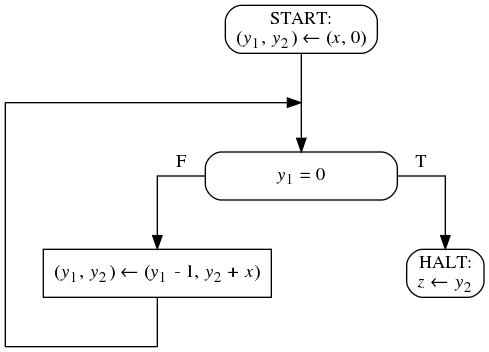
ϕ(x) ≡ x ≥ 0, ψ(x, z) ≡ z = x²ϕ(x) ≡ T, ψ(x, z) ≡ z = x²ϕ(x) ≡ |x| > 10, ψ(x, z) ≡ |z| > 100ϕ(x) ≡ x > 0, ψ(x, z) ≡ z > xϕ(x) ≡ x ≥ 0, ψ(x, z) ≡ z ≥ x
- Для каждой приведенной ниже спецификации напишите блок-схемы с указанными ниже свойствами, если они существуют. Домен всех входных и выходных переменных - множество всех целых чисел.
- блок-схема, не являющая частично корректной относительно данной спецификации;
- блок-схема, являющаяся частично, но не полностью корректной относительно данной спецификации, при этом блок-схема должна завершаться на всем подмножестве входного домена, для которого существует элемент выходного домена, удовлетворяющий постусловию;
- блок-схема, являющаяся полностью корректной относительно данной спецификации.
ϕ(x₁, x₂) ≡ x₁ > x₂ ≥ 0, ψ(x₁, x₂, z₁, z₂) ≡ z₁ > x₁ > z₂ > x₂ϕ(x₁, x₂) ≡ 0 > x₁ > x₂, ψ(x₁, x₂, z₁, z₂) ≡ x₁² > z₁ > x₂² > z₂ϕ(x₁, x₂) ≡ x₁ > x₂ ≥ 0, ψ(x₁, x₂, z₁, z₂) ≡ x₂² > z₁ > x₁² > z₂ϕ(x₁) ≡ x₁ > 0, ψ(x₁, z₁, z₂) ≡ z₁ = x₁ * z₂ ∧ z₁ < z₂
- Докажите или опровергните утверждения о {частичной} или ❬полной❭ корректности. Заглавными буквами обозначены блок-схемы, строчными - логические формулы.
∀ a ∀ P ∃ b such as {a}P{b} ⇒ {b}P{a}∀ a ∀ P ∃ b such as ❬a❭P❬b❭ ⇒ {b}P{a}∀ P ∃ a ∃ b such as ❬a❭P❬b❭∀ P ∃ a ∃ b such as {a}P{b} ∧ ¬ ❬a❭P❬b❭
