Практикум -- задание №1
Это задание состоит из 3-х частей. Нужно выполнить все части.
Задание 1.1
- Установите инструменты Frama-C, Why3, AstraVer и солверы согласно инструкции. Устанавливать Coq и CoqIDE не нужно. Установите солвер CVC4 инструкция
- Познакомьтесь с языком Why3 по этому документу. Обратите внимание, что в нем описывается язык версии 0.88.2, а наши инструменты поддерживают версию 0.87. Часть синтаксиса изменилась.
-
Ниже описаны программы
P1иP2и требованияT1иT2.- Реализуйте (на листочке) программы
P1иP2на языке Си (например, как функции). - Промоделируйте (на листочке) программы
P1иP2в виде блок-схем. Все переменные блок-схем должны иметь домен всех целых чисел. Модель должна быть составлена по программе «механически», «синтаксически», т.е. ее соответствие программе должно быть очевидно. - Промоделируйте (на листочке) требования
T1иT2в виде предусловий и постусловий. - Определите все пары программ и требований, которые находятся в отношении частичной корректности. Докажите эти факты (на листочке).
- Определите все пары программ и требований, которые находятся в отношении полной корректности. Докажите эти факты (на листочке).
- Оформите каждое доказательство в виде теории Why3. Цель теории – доказать нужное отношение соответствия. Результат вашей работы – это архив следующего состава: файл со всеми теориями, сессия доказательства всех теорий, программы на Си, фото блок-схем и фото доказательств с листочка. В начале файла с теориями поместите комментарий, обосновывающий отсутствие частичной корректности и полной корректности для всех пар программ и требований, не включенных в файл.
- Реализуйте (на листочке) программы
Входом Программы P1 являются три целых числа, выходом – одно число. Программа отнимает от первого числа третье и затем прибавляет к полученному второе число. Так получается выходное число.
Все вычисления делаются в машинной арифметике в целых числах от -231 до 231 - 1 (нет вычислений в других типах целых чисел). Сумма и вычитание – это бинарные операции над такими целыми числами, их результаты – такие же числа. Операции не определены для случая переполнения: каждое сложение и вычитание в программе на Си должно моделироваться как проверка результата и зацикливание в случае переполнения. Постарайтесь не делать лишних действий в программе на Си (учитывайте наличие предусловия и ситуации неопределенного поведения в языке Си).
Входы и выходы Программы Р2 те же, что и у Программа Р1. Ее цель – вычислить то же выражение. Она сравнивает значения входных чисел и выбирает такой порядок суммы и вычитания, чтобы не случилось переполнение всегда, когда лишь результат всего искомого выражения представим данными целыми числами. Попробуйте самостоятельно составить такую программу. Она использует ту же машинную арифметику, что и Программа Р1.
Требования Т1 применимы к программам с тремя входными переменными (назовем их x1, x2, x3) и одной выходной переменной. Домены всех переменных – множество всех целых чисел. Программа должна вычислять значение выражения x1 + x2 - x3. Программа не должна зацикливаться или вычислять другое значение, если значения всех входных переменных принадлежат множеству от -231 до 231 - 1 включительно, а значения выражений x1 - x3 и x1 + x2 - x3 представимы в типе указанных выше ограниченных целых чисел.
Требования Т2 применимы к программам с тремя входными переменными (назовем их x1, x2, x3) и одной выходной переменной. Домены всех переменных – множество всех целых чисел. Программа вычисляет значение выражения x1 + x2 - x3. Программа не должна зацикливаться или вычислять другое значение, если значения входных переменных принадлежат множеству от -231 до 231 - 1 включительно, а значение выражения x1 + x2 - x3 представимо в типе указанных выше ограниченных целых чисел.
Прагматика Это задание знакомит вас со средой верификации, которой вы будете пользоваться в дальнейшем для верификации Си-программ. Конкретнее, по Си-программе и спецификации к ней будут строиться утверждения, означающие правильность программы. Утверждения будут строиться на языке Why3 и доказываться в среде Why3 IDE. Знание этого языка вам потребуется, чтобы читать и понимать утверждения, которые будут генерировать инструменты верификации. Среда Why3 IDE дает возможность использовать сразу несколько солверов для верификации. Они отличаются языками, на которых нужно записывать доказываемые утверждения, способами запуска и управления. Разобраться со всеми этими отличиями берет на себя среда Why3 IDE. Вам она предоставляет унифицированный интерфейс управления солверами и единый язык (Why3), который она сама будет транслировать во входные языки солверов.
Задание 1.2
Вам дана блок-схема и спецификация к ней. При помощи метода индуктивных утверждений докажите частичную корректность этой блок-схемы относительно этой спецификации. Результатом вашей работы будет такой же архив, как и в задании 1.1. На фото блок-схемы укажите точки сечения. Индуктивные утверждения оформите в виде предикатов.
Множество переменных V = { x, y1,
y2, y3, z } состоит
из одной входной, трех промежуточных и одной выходной переменных.
Доменом всех переменных является множество всех целых чисел.
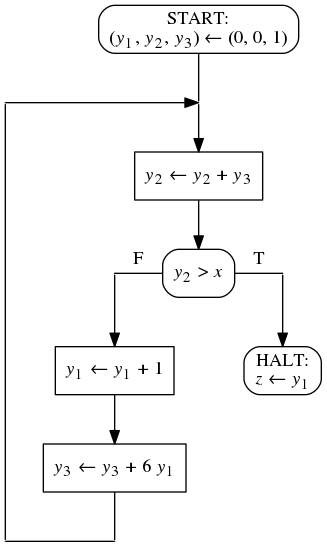
На рисунке представлена блок-схема программы над множеством переменных
V, вычисляющая целую часть кубического корня.
ϕ(x) ≡ x ≥ 0
ψ(x, z) ≡ z3 ≤ x < (z + 1)3
Прагматика Это задание позволяет отработать метод индуктивных утверждений. Он потребуется вам, чтобы верифицировать Си-программы с циклами.
Задание 1.3
Вам дана блок-схема и спецификация к ней. При помощи метода фундированных множеств докажите завершаемость этой блок-схемы относительно этой спецификации. Результатом вашей работы будет такой же архив, как и в задании 1.1. На фото блок-схемы укажите точки сечения. Фундированное множество, индуктивные утверждения и оценочные функции оформите соответствующим способом в файле с теориями. Не забудьте доказать фундированность множества (это тоже будут цели).
Множество переменных V = { x, y1,
y2, y3, z } состоит
из одной входной, трех промежуточных и одной выходной переменных.
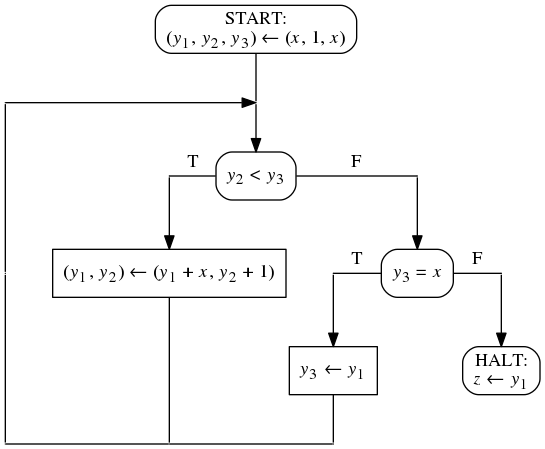
Доменом всех переменных является множество всех целых чисел. На рисунке
представлена блок-схема программы над множеством переменных V.
ϕ(x) ≡ x > 1
Прагматика Это задание позволяет отработать метод фундированных множеств. Он потребуется вам, чтобы доказывать завершаемость Си-программ с циклами.