- Вам дана блок-схема над 1 входной, 2 промежуточными
и 1 выходной переменной. Домены всех переменных - множество
всех целых чисел. Вам дана спецификация над этими же
переменными. При помощи методов Флойда докажите, что
блок-схема полностью корректна относительно спецификации.
ϕ(x) ≡ x > 0
ψ(x, z) ≡ z > x
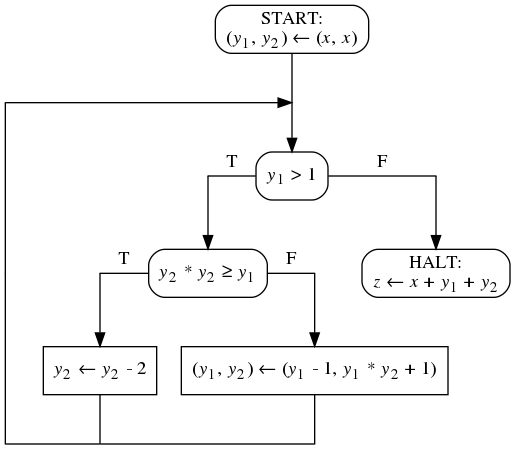
- Вам дана блок-схема над 1 входной, 2 промежуточными
переменными. Домены всех переменных - множество всех целых
чисел. Вам дано предусловие над этими же переменными.
При помощи методов Флойда докажите, что блок-схема
завершается на этом предусловии.
ϕ(x) ≡ x ≥ 0
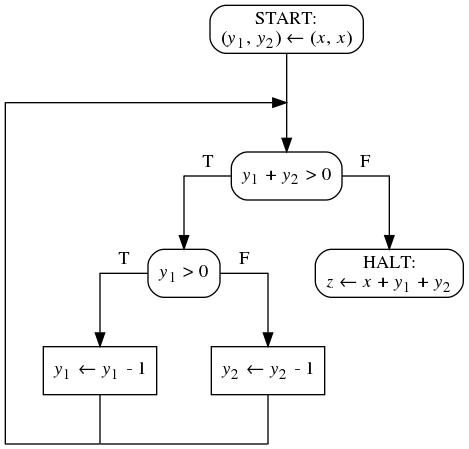
- Вам дана блок-схема над 1 входной, 2 промежуточными
переменными. Домены всех переменных - множество всех
целых чисел. Вам дано предусловие над этими же переменными.
При помощи методов Флойда докажите, что блок-схема
завершается на этом предусловии.
ϕ(x) ≡ x ≥ 0
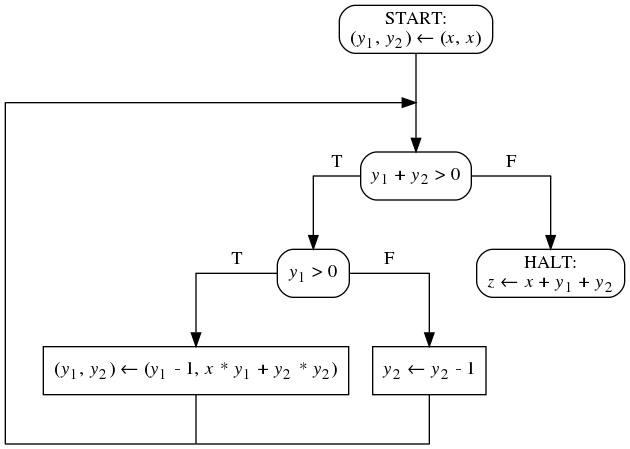
- Вам дана блок-схема над 1 входной, 2 промежуточными
переменными. Домены всех переменных - множество всех
целых чисел. Вам дано предусловие над этими же переменными.
При помощи методов Флойда докажите, что блок-схема
завершается на этом предусловии.
ϕ(x) ≡ x > 0
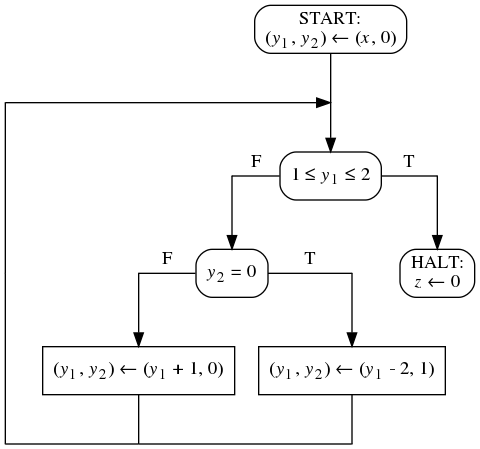
- Пусть у нас есть блок-схема и предусловие. Завершаемость
блок-схемы на этом предусловии доказана по методу
фундированных множеств с выбранным фундированным
множеством
(U, a) и выбранными оценочными функциями
ui. Возможно ли доказать завершаемость
тем же методом с использованием тех же точек сечения и
тождественных функций в качестве оценочных? Если да,
то сделайте это на каком-нибудь примере и для всех случаев.



