1. Пусть вам дали некоторую блок-схему и спецификацию к ней. Вы знаете метод индуктивных утверждений Флойда, т.е. умеете предлагать инварианты циклов и при помощи них доказывать частичную корректность. Данная вам блок-схема, как оказалось, не является частично корректной. Но вы уже видите инварианты циклов. Можно ли их использовать для конструктивного доказательства некорректности блок-схемы? То есть поиска значений входных переменных, на которых предусловие выполнено и блок-схема не зацикливается, но значения выходных переменных не удовлетворяют постусловию?
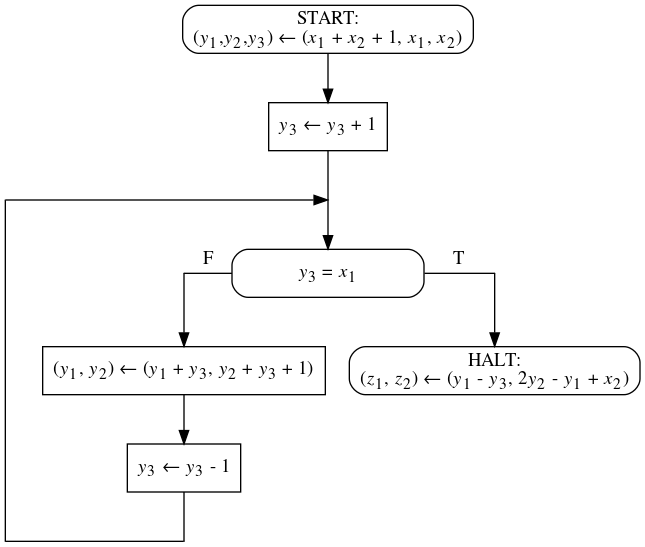
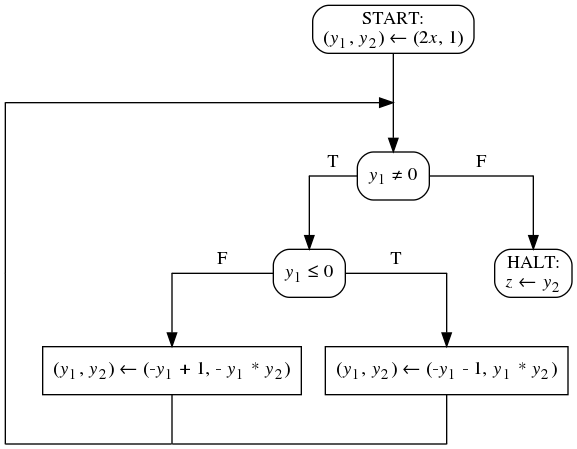
  2. Вам дана блок-схема над 2 входными, 3 промежуточными и 2 выходными переменными. Домены всех переменных - множество всех целых чисел. Вам дана спецификация над этими же переменными. При помощи метода индуктивных утверждений докажите, что блок-схема частично корректна относительно спецификации. ϕ(x₁, x₂) ≡ x₂ ≥ 0 ψ(x₁, x₂, z₁, z₂) ≡ z₁ - x₁ = z₂ - x₂ (блок-схема к задаче)
  3. Вам дана блок-схема над 1 входной, 2 промежуточными и 1 выходной переменными. Домены всех переменных - множество всех целых чисел. Вам дана спецификация над этими же переменными. При помощи метода индуктивных утверждений докажите, что блок-схема частично корректна относительно спецификации. ϕ(x) ≡ x ≥ 0 ψ(x, z) ≡ z = (2x)! (блок-схема к задаче)
  4. Какое требуется минимальное число точек сечения, чтобы доказать частичную корректность хотя бы одной блок-схемы, имеющей указанные особенности, относительно хотя бы одной спецификации при помощи методов Флойда, если блок-схемы с указанными особенностями существуют. Если ответ зависит от спецификации, привести не менее двух разных ответов и обосновать их.
    1. блок-схема содержит 2 цикла;
    2. блок-схема содержит не менее одного оператора соединения;
    3. блок-схема зацикливается на всех значениях входных данных из своих доменов;
    4. операторы и связки блок-схемы разбиваются на 3 независимые связные части так, что первая и вторая часть обладают единственной общей связкой, вторая и третья часть обладают единственной общей связкой, а первая и третья часть не обладают общими связками. Общих операторов у частей нет.